(注)このページの図は動きません
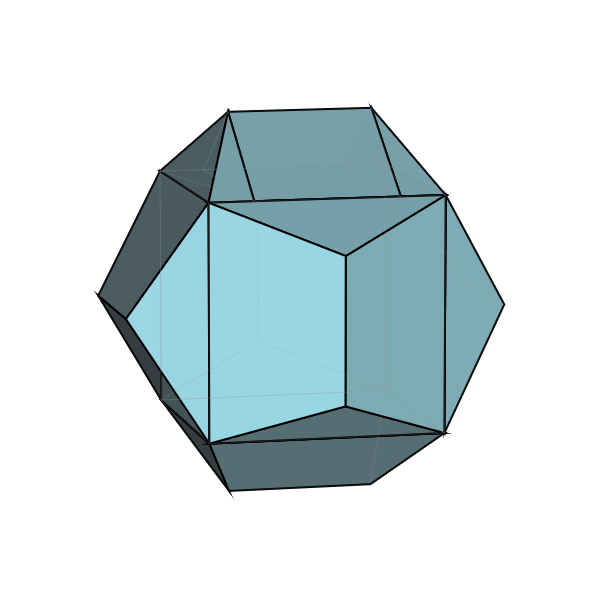
正12面体は立方体の6つの面のそれぞれに「屋根」をつけた形となります。
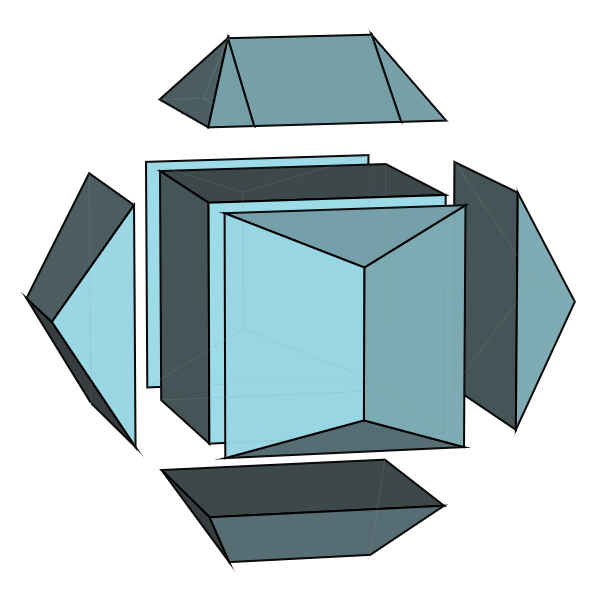
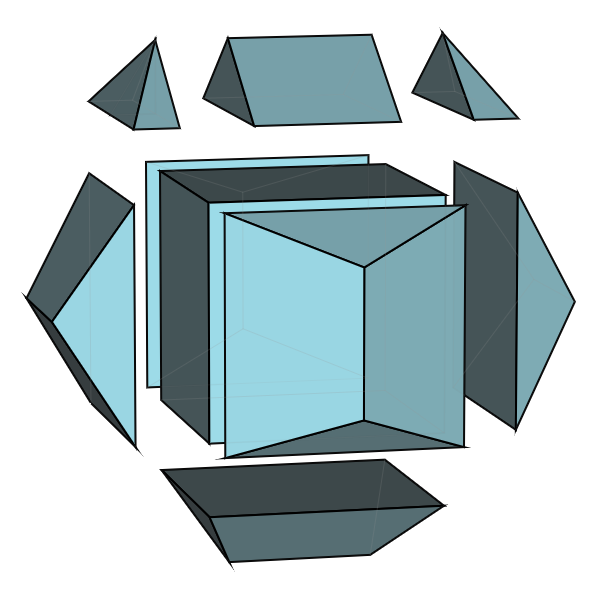
「屋根」は両端の四角錐と中央の三角柱に分けられます。(立方体の面と垂直に切断する)
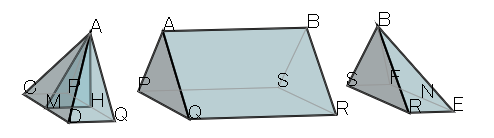
頂点A,Bを含む「屋根」をA,Bを通り立方体の面に垂直に切断し、3つの部分に分けます。
切断面と辺DE,CFの交点を図のようにQ,R,P,Sとします。また,MはCDの中点,HはAから面CDEFに下ろした垂線の足です。
\(最初に端の四角錐A-CDQPの体積V_1を求めます。\)
QRは正五角形の1辺であるABと等しく,DEはその正五角形の対角線であるから
\(QR=1,DE=\frac{\sqrt{5}+1}{2}\)
\(DQ=(DE-QR)/2=(\frac{\sqrt{5}+1}{2}-1)÷2=\frac{\sqrt{5}-1}{4}\)
また、△ACMに三平方の定理を用いると,AM>0であるから\(AM=\sqrt{AC^2-CM^2}=\sqrt{1^2-(\frac{1+\sqrt{5}}{4})^2}=\frac{\sqrt{10-2\sqrt{5}}}{4}\)
さらに△AMHに三平方の定理を用いると,AH>0であるから\(AH=\sqrt{AM^2-MH^2}=\sqrt{(\sqrt{\frac{10-2\sqrt{5}}{4}})^2-(\frac{(\sqrt{5}-1)^2}{4})^2}\)
\(=\sqrt{\frac{(10-2\sqrt{5})-(5-2\sqrt{5}+1)}{16}}=\sqrt{\frac{1}{4}}=\frac{1}{2}\)
\(したがって四角錐の体積V_1は\)\(V_1=\frac{1}{3} \cdot CD \cdot DQ \cdot AH=\frac{1}{3}\cdot \frac{\sqrt{5}+1}{2}\cdot \frac{\sqrt{5}-1}{4}\cdot \frac{1}{2}=\frac{1}{12}\)
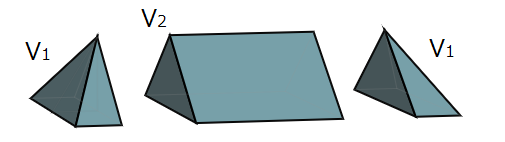
\(次に中央の三角柱の体積V_2を求めます。\)
\(V_2=\triangle{APQ}\cdot PR=\frac{1}{2}PQ\cdot AH \cdot PR = \frac{1}{2}\cdot \frac{\sqrt{5}+1}{2}\cdot \frac{1}{2}\cdot 1=\frac{\sqrt{5}+1}{8}\)
\(屋根の体積V_3は\)\(V_3=V_1×2+V_2=\frac{1}{12} \times 2 + \frac{\sqrt{5}+1}{8}=\frac{1}{6}+\frac{\sqrt{5}+1}{8}\)
\(立方体の体積をV_0とすると\)
\(V_0=(\frac{\sqrt{5}+1}{2})^3=\sqrt{5}+2\)
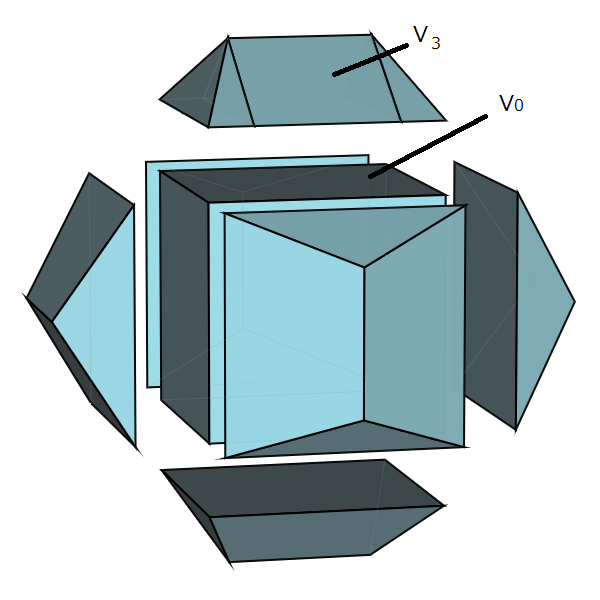
したがって、1辺が1の正十二面体の体積V'は
\(V'=V_0+6V_3=2+\sqrt{5}+6\times( \frac{1}{6}+\frac{\sqrt{5}+1}{8})=2+\sqrt{5}+1+\frac{3\sqrt{5}+3}{4}=\frac{15+7\sqrt{5}}{4}\)
\(1辺の長さがaの正十二面体の体積をVとすると,V':V=1:a^3であるから\) \(V=\frac{15+7\sqrt{5}}{4}a^3\)