2019東工大　数学　第4問

\( H_1,\cdots,H_n を相異なるn枚の平面とする。\)

\( H_1,\cdots,H_n によって空間が T(H_1,\cdots,H_n)個の空間領域に分割されるとする。\)

例えば、\(空間の座標を(x,y,z)とするとき、\)

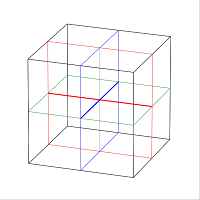
\( ●平面x=0をH_1,平面y=0をH_2,平面z=0をH_3とするとT(H_1,H_2,H_3)=8\)

（画像をクリック)

\( ●平面x=0をH_1,平面y=0をH_2,平面x+y=1をH_3とするとT(H_1,H_2,H_3)=7\)

（画像をクリック)

\( ●平面x=0をH_1,平面x=1をH_2,平面y=0をH_3とするとT(H_1,H_2,H_3)=6\)

（画像をクリック)

\( ●平面x=0をH_1,平面y=0をH_2,平面z=0をH_3,平面x+y+z=1をH_4とするとT(H_1,H_2,H_3,H_4)=15\)

（画像をクリック)

である。 \( (1)各nに対してT(H_1,\cdots,H_n)の取りうる値のうち、最も大きいものを求めよ。\) \( (2)各nに対してT(H_1,\cdots,H_n)の取りうる値のうち、2番目に大きいものを求めよ。ただし、n\geqq 2とする。\) \( (3)各nに対してT(H_1,\cdots,H_n)の取りうる値のうち、3番目に大きいものを求めよ。ただし、n\geqq 3とする。\)