ひねり四角柱の体積
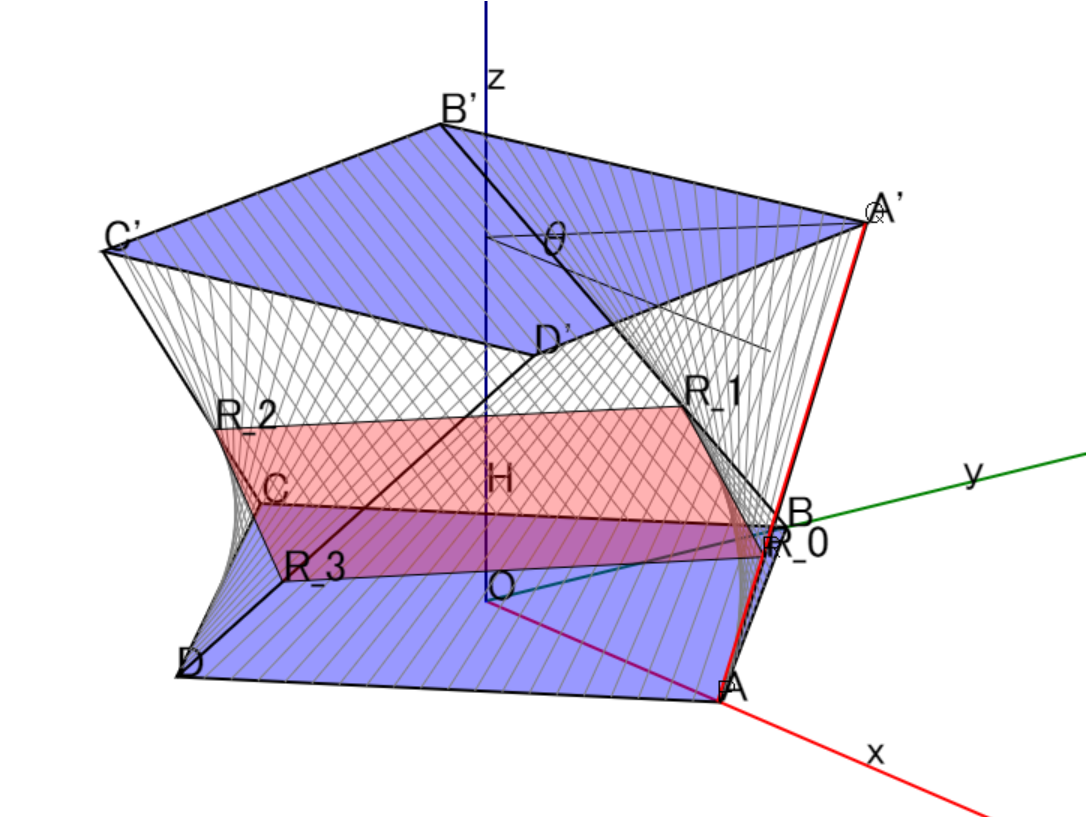
座標空間内に4点$\rm{A}(1,0,0),\rm{B}(0,1,0),\rm{C}(-1,0,0),\rm{D}(0,-1,0)$がある。
この4点を原点$\rm{O}$を中心として$z$軸まわりに$\rm OA$から$\rm OB$の方向へ$\theta$だけ回転させ,さらに$z$軸方向に1だけ平行移動した点をそれぞれ$\rm A',B',C',D'$とする。
点$\rm P$は点$\rm{A}$を出発し,$\rm{A}\rightarrow \rm{B} \rightarrow \rm{C} \rightarrow \rm{D} \rightarrow \rm{A}$の順に動く。
点$\rm Q$は点$\rm{A'}$を出発し、$\rm{A'}\rightarrow \rm{B'} \rightarrow \rm{C'} \rightarrow \rm{D'} \rightarrow \rm{A'}$の順に動く。
点$\rm P,Q$は同時に$\rm A,A'$を出発し、同じ速さで移動する。
このとき,2つの正方形$\rm ABCD,A'B'C'D'$と線分$\rm PQ$が通過する曲面で囲まれた立体をKとする。
(1) 立体$\rm K$と平面$z=h (0< h< 1)$の共通部分が正方形になることを示せ。
(2) 立体$\rm K$の体積を$\theta $を用いて表せ。
(解)
(1)まず,点Pが線分AB上,点Qが線分$\rm{A'B'}$上を動くときを考える。点$\rm{A,B,A',B',P,Q}$の位置ベクトルをそれぞれ$\overrightarrow{a},\overrightarrow{b},\overrightarrow{a'},\overrightarrow{b'},\overrightarrow{p},\overrightarrow{q}$とする。
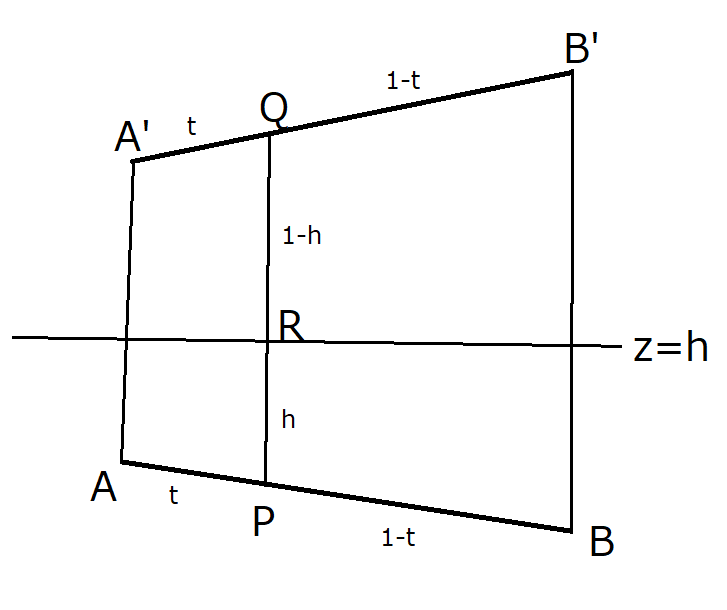
点PがAB上にあるとき、変数tを用いて、
$\overrightarrow{p}=(1-t)\overrightarrow{a}+t\overrightarrow{b} (0< t < 1)$と表せる。
このとき、点Qは$\rm A'B'$上にあり、$\overrightarrow{q}=(1-t)\overrightarrow{a'}+\overrightarrow{b'}$である。
線分PQと平面$z=h (0< h < 1)$の共有点を$\rm{R}(\overrightarrow{r})$とする。$\rm PR:QR$ =$h:(1-h)$であるから、
$\overrightarrow{r}=(1-h)\overrightarrow{p}+h \overrightarrow{q}$となる。
したがって、
\begin{eqnarray*}
\overrightarrow{r}&=&(1-h)\{(1-t)\overrightarrow{a}+t\overrightarrow{b}\}+h\{(1-t)\overrightarrow{a'}+t(\overrightarrow{b'})\} \\
&=&
(1-h)(1-t)\overrightarrow{a}+(1-h)t\overrightarrow{b}+h(1-t)\overrightarrow{a'}+ht\overrightarrow{b'} \\
&=&(1-t)\{(1-h)\overrightarrow{a}+h\overrightarrow{a'}\}+t\{(1-h)\overrightarrow{b}+h\overrightarrow{b'}\}
\end{eqnarray*}
ここで,~$\rm AA',BB'$をそれぞれ$h:(1-h)$に内分する点を
$\rm R_0(\overrightarrow{r_0}),R_1(\overrightarrow{r_1})$とすると
$\overrightarrow{r}=(1-t)\overrightarrow{r_0}+t\overrightarrow{r_1}$
となり、点$\rm R$は線分$\rm{R_0R_1}$を動くことが分かる。
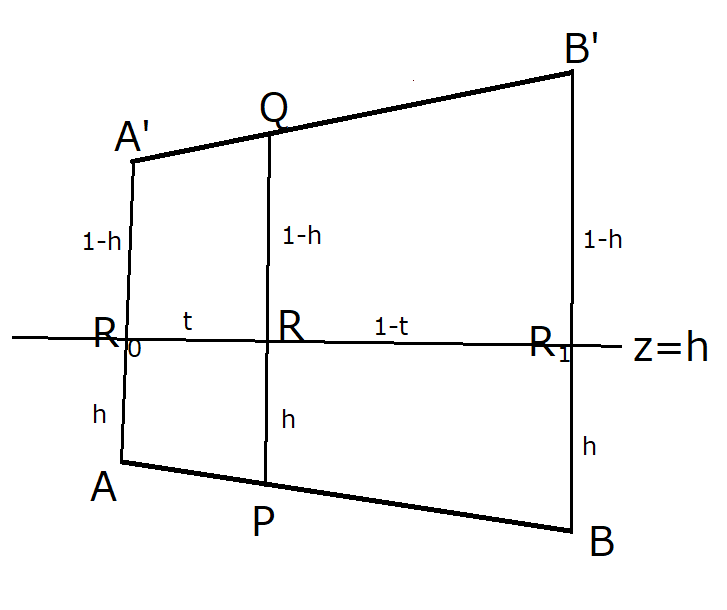
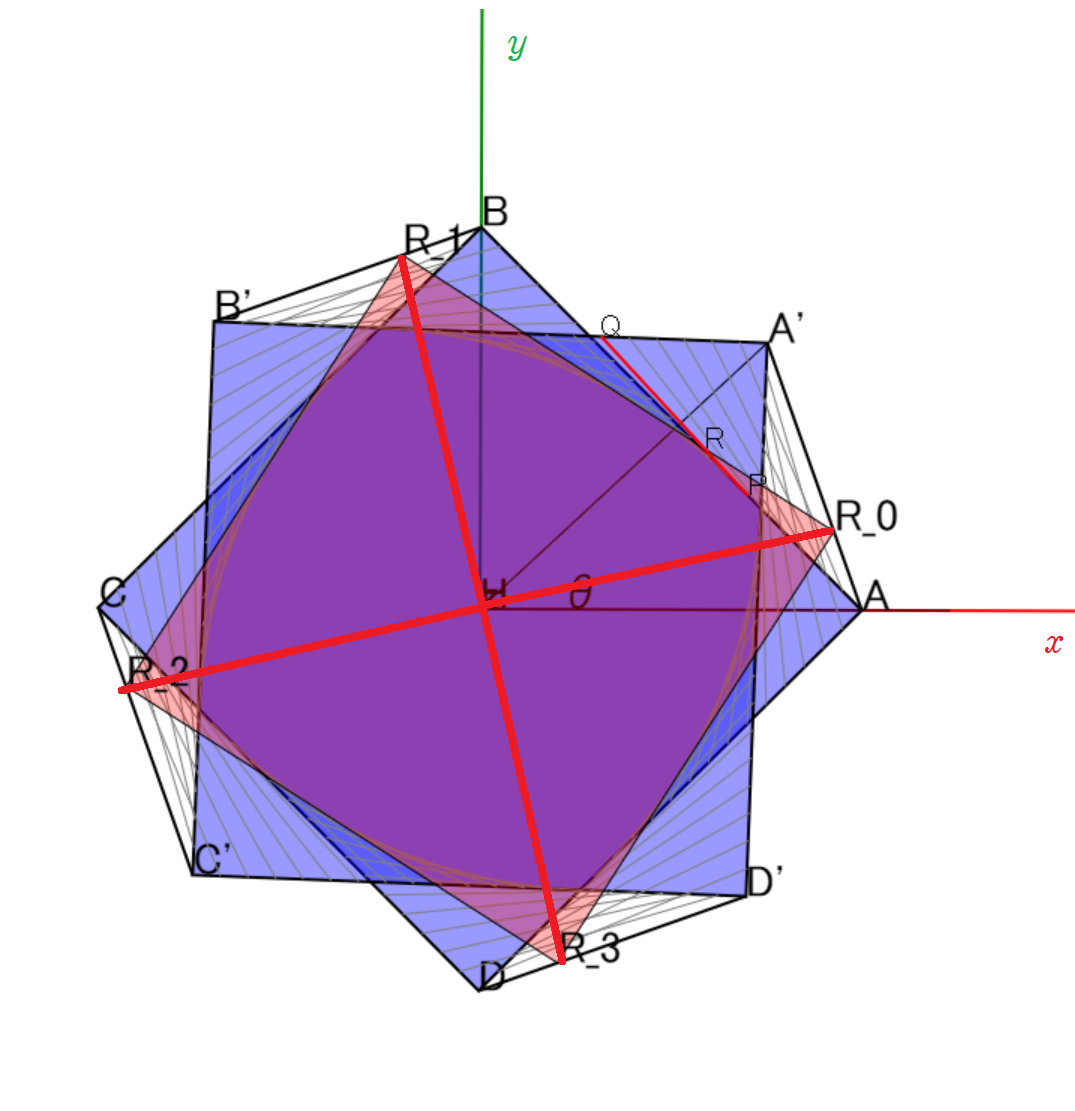
次に点$\rm P$が線分$\rm BC,CD,DA$上を動くときを考える。$\rm CC',DD'$を$h:(1-h)$に内分する点を$\rm R_2,R_3$とすると,~点$\rm R$は線分$\rm{R_1R_2},\rm{R_2R_3},~\rm{R_3R_1}$を動く。
3点$\rm{R_1,R_2,R_3}$は$\rm R_0$をそれぞれ$\displaystyle \frac{\pi}{2},\pi,\frac{3\pi}{2}$だけz軸周りに回転移動したものであるから、四角形$\rm R_0R_1 R_2 R_3$は正方形になる。したがって、平面$z=h$と立体$\rm K$の共通部分は正方形となる。
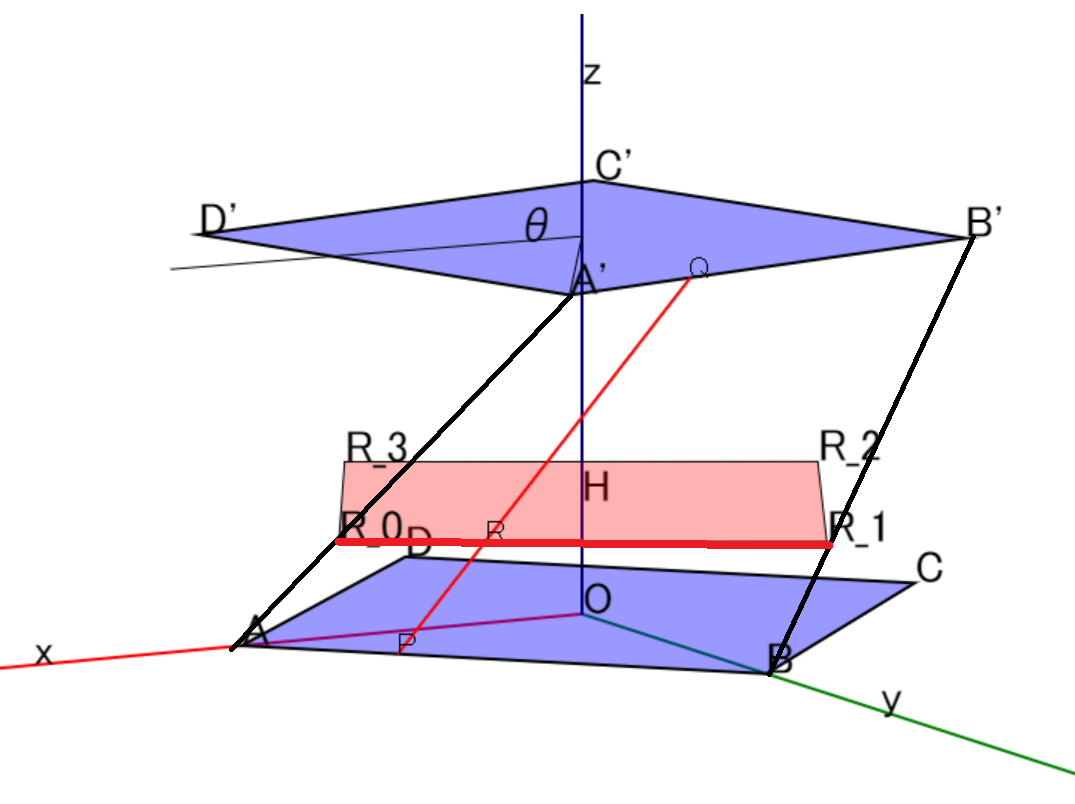
(2) $\rm{A'}$の座標は$(\cos \theta, \sin \theta,h$)と表せるから、
\begin{eqnarray*}
\overrightarrow{\rm{OR_0}}&=&(1-h)\overrightarrow{a}+h\overrightarrow{a'} \\
&=&(1-h,0,0)+h(\cos \theta ,\sin \theta,h) \\
&=&(1-h+h \cos \theta, h \sin \theta,h) \\
\end{eqnarray*}
$z$軸と平面$z=h$の交点を${\rm H}(0,0,h)$とすると
\begin{eqnarray*}
\overrightarrow{\rm{HR_0}}=(1-h)\overrightarrow{a}+h\overrightarrow{a'} =(1-h+h \cos \theta, h \sin \theta,0)
\end{eqnarray*}
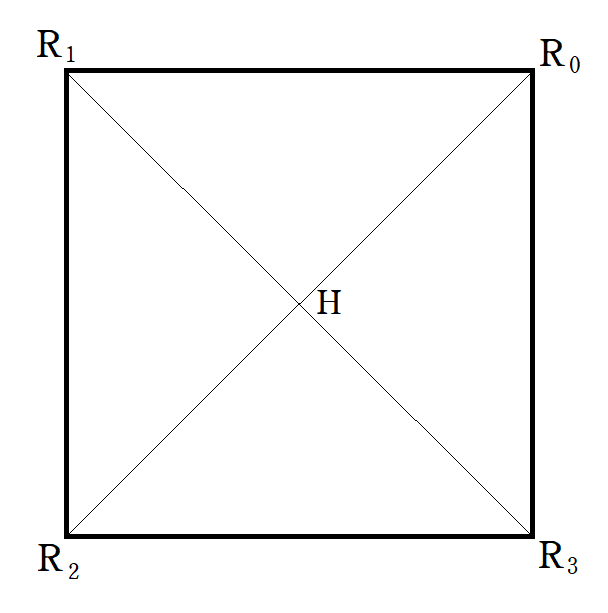
$\overrightarrow{\rm{HR_0}}$は正方形$\rm R_0R_1R_2R_3$の対角線の半分であるから,断面積$S(h)$は次のようになる。
\begin{eqnarray*}
S(h)&=&2|\rm{\overrightarrow{\rm{HR_0}}}|^2 \\
&=&2\{(1-h+h\cos \theta)^2+(h \sin \theta)^2 + (h-h)^2\} \\
&=& 2\{1^2+h^2+h^2\cos \theta - 2h -2h^2 \cos \theta+ 2h \cos \theta + h^2 {\sin}^2 \theta\} \\
&=& 2\{h^2({\sin}^2 \theta + {\cos}^2 \theta) +h^2-2h \cos \theta +2h \cos \theta -2h +1\} \\
&=& 2\{2h^2-2h^2\cos \theta + 2h \cos \theta -2h+1\}\\
&=& 2\{2(1-\cos \theta)h^2 -2h(1-\cos \theta)+1\} \\
&=&4(1-\cos \theta) h^2-4(1-\cos \theta) h+ 2
\end{eqnarray*}
立体$\rm K$の体積を$V$とする。$V$は$S(h)$を$h=0$から1まで積分することで求めることができる。
\begin{eqnarray*}
V &=& \int_0 ^1 S(h) dh\\
&=& \int_0 ^1 \{4(1-\cos \theta)h^2 -4(1-\cos \theta)h+2\} dh\\
&=& 4(1-\cos \theta)\int_0^1 (h^2-h)dh + 2\int_0^1 dh\\
&=& 4(1-\cos \theta)\left[\frac{1}{3}h^3 -\frac{1}{2}h^2\right]_0^1 +2\biggl[h\biggr]_0^1\\
&=& 4(1-\cos \theta)\left(\frac{1}{3}-\frac{1}{2}\right)+2\\
&=& 4(1-\cos \theta)\left(-\frac{1}{6}\right)+2\\
&=& \frac{2}{3}(2+\cos \theta)
\end{eqnarray*}
(考察)
四角柱の体積を$V$とする。またこの四角柱の上面を$\theta$捻じった立体(上面、底面、その2つの面の対応する点を結んだ線分によって囲まれる立体)の体積を$V'$とする。$V'$を$V$と$\theta$を用いて表すと$$ V'=\frac{1}{3}(2+\cos \theta)V$$となる。
$\theta = 0$のときは四角柱のままで$V'=V$である。
$\theta = \pi$ のとき$\displaystyle V'=\frac{1}{3}V$となりこれは四角錐の体積と一致する。
また,$\displaystyle \theta = \frac{1}{3}\pi$のとき,$\displaystyle V'=\frac{1}{2}V$となることが分かる。






